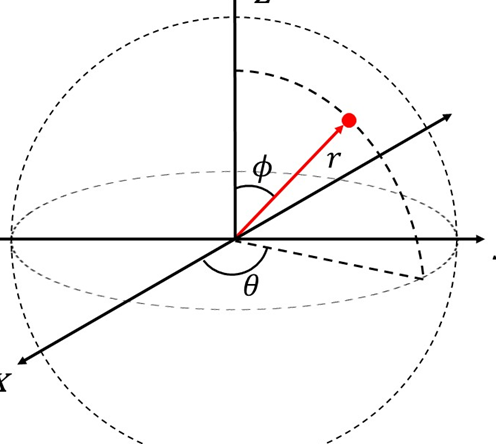
Descubre el significado del ángulo polar en matemáticas
En matemáticas, el ángulo polar es una medida angular utilizada en coordenadas polares para describir la posición de un punto en un plano. Se define como el ángulo formado por el eje polar positivo y la línea que une el punto con el origen de coordenadas. Este concepto es fundamental en trigonometría y geometría analítica, ya que permite representar de manera eficiente puntos en un plano utilizando magnitudes angulares y radiales.
La importancia del ángulo polar en matemáticas
El ángulo polar es esencial para la descripción de coordenadas polares, un sistema de coordenadas alternativo al sistema cartesiano que facilita la representación de figuras complejas y la resolución de problemas en geometría y física. Al utilizar el ángulo polar, podemos expresar de forma única la ubicación de un punto en relación con el eje polar y la distancia al origen, lo que simplifica cálculos y visualizaciones.
Descubre la razón detrás del nombre de coordenadas polares
Las coordenadas polares reciben su nombre precisamente por la utilización del ángulo polar como componente principal en su representación. Al contrario de las coordenadas cartesianas, que se basan en ejes perpendiculares (x, y), las coordenadas polares emplean un eje radial (distancia al origen) y un ángulo polar (dirección desde el eje polar).
Origen histórico de las coordenadas polares
El sistema de coordenadas polares tiene sus raíces en las contribuciones de matemáticos como Isaac Newton y Leonhard Euler, quienes desarrollaron métodos para representar funciones y figuras geométricas de manera más eficiente que con coordenadas cartesianas tradicionales. La introducción del ángulo polar en este sistema permitió simplificar operaciones trigonométricas y visualizar patrones en el plano de forma más intuitiva.
Descubre el significado del ángulo polar en geometría
En geometría, el ángulo polar se utiliza para determinar la orientación de un vector o segmento de recta en relación con el eje polar. Esta medida angular es fundamental para entender rotaciones, reflexiones y traslaciones en el plano, así como para analizar simetrías y transformaciones geométricas.
Relación entre ángulo polar y coordenadas cartesianas
En el contexto de coordenadas polares, el ángulo polar se relaciona con las coordenadas cartesianas (x, y) a través de las fórmulas de conversión trigonométrica. Esta conexión entre sistemas de referencia permite traducir entre coordenadas rectangulares y polares, lo que resulta útil en problemas de cálculo integral, física y geometría analítica.
¿Qué es una posición polar y cómo se define?
Una posición polar se refiere a la ubicación de un punto en un plano bidimensional mediante el uso de coordenadas polares. Esta posición se define por dos elementos: la distancia al origen (r) y el ángulo polar (θ). La combinación de estos dos valores permite determinar de manera única la localización de un punto en el plano, lo que resulta útil en diversas aplicaciones matemáticas y físicas.
Características de una posición polar
En una posición polar, la distancia al origen (r) representa la magnitud o módulo del vector que une el punto con el origen de coordenadas, mientras que el ángulo polar (θ) indica la dirección o inclinación de dicho vector respecto al eje polar. Estos dos elementos son independientes entre sí, lo que significa que un punto puede tener diferentes coordenadas polares que representen la misma posición en el plano.
Preguntas frecuentes sobre el ángulo polar y coordenadas polares
1. ¿Cuál es la diferencia entre un ángulo polar y un ángulo en coordenadas cartesianas?
En coordenadas polares, el ángulo polar se mide desde el eje polar y se cuenta en sentido contrario a las agujas del reloj, mientras que en coordenadas cartesianas, el ángulo se mide respecto al eje x positivo en sentido antihorario.
2. ¿Por qué se prefiere usar coordenadas polares en ciertos problemas matemáticos?
Las coordenadas polares son especialmente útiles para describir fenómenos con simetría circular o radial, como ondas, espirales y campos vectoriales, ya que simplifican las expresiones matemáticas y facilitan la visualización de patrones geométricos.
3. ¿Cómo se calcula la distancia entre dos puntos en coordenadas polares?
Para hallar la distancia entre dos puntos dados en coordenadas polares, se puede aplicar la fórmula de la distancia euclidiana, que combina las coordenadas radiales y los ángulos polares de los puntos para determinar la longitud del segmento que los une.
4. ¿Cuál es la relación entre coordenadas cilíndricas y coordenadas polares en tres dimensiones?
Las coordenadas cilíndricas extienden el concepto de coordenadas polares al espacio tridimensional, añadiendo una tercera componente (altura z) a las coordenadas radiales y angulares. Este sistema es usado en física y geometría para describir objetos con simetría cilíndrica.
5. ¿Cómo se utilizan las coordenadas polares en aplicaciones de ingeniería y diseño?
En ingeniería y diseño, las coordenadas polares son empleadas para representar curvas y trayectorias circulares, así como para modelar rotaciones y movimientos en sistemas mecánicos y estructurales. Su simplicidad y versatilidad las hacen una herramienta valiosa en el análisis de problemas complejos.