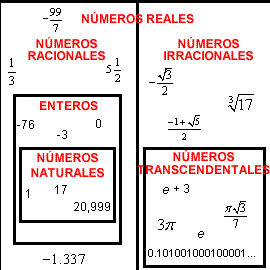
Descubre la razón detrás del nombre de los irracionales
Los números irracionales son aquellos que no pueden ser expresados como una fracción o cociente de dos números enteros. La palabra «irracional» en este contexto no se refiere a la falta de lógica o sentido común, sino a la imposibilidad de expresar estos números de manera «racional» con fracciones.
Origen del término «irracional»
El término «irracional» en el contexto de los números fue introducido por los antiguos matemáticos griegos, quienes se encontraron con la existencia de números que no podían ser expresados como razones o fracciones simples. Estos números parecían desafiar la lógica matemática de la época, lo que llevó a denominarlos como «irracionales».
La peculiaridad de los números irracionales
Los números irracionales presentan propiedades únicas y fascinantes en el mundo de las matemáticas. A diferencia de los números enteros y racionales que pueden ser representados de manera exacta, los irracionales son infinitos y no periódicos en su representación decimal.
Descubre qué es un número irracional en matemáticas
En matemáticas, un número irracional es aquel que no puede ser expresado de forma exacta como una fracción. Ejemplos clásicos de números irracionales son √2, π (pi) y e (número de Euler). Estos números tienen infinitas cifras decimales no periódicas y su representación decimal es no repetitiva.
Propiedades de los números irracionales
Los números irracionales son no repetitivos, lo que significa que su expansión decimal nunca se detiene ni se repite en un patrón fijo. Esta característica los distingue de los números racionales, cuyas expansiones decimales son finitas o periódicas.
Relación con la geometría
Los números irracionales están estrechamente relacionados con la geometría y la medida de ciertas figuras. Por ejemplo, la diagonal de un cuadrado cuyo lado mide 1 unidad es un número irracional (√2), lo que demuestra la presencia de estos números en situaciones cotidianas y teóricas.
Descubre la conclusión de los números irracionales
En el ámbito matemático, los números irracionales son fundamentales para completar el conjunto de números reales. La existencia de estos números demuestra la riqueza y complejidad del universo matemático, ampliando las posibilidades de representación y cálculo en diversas áreas de las matemáticas.
Aplicaciones en la física y la ingeniería
Los números irracionales son utilizados en disciplinas como la física y la ingeniería para modelar fenómenos naturales y realizar cálculos precisos. Su presencia en ecuaciones y fórmulas demuestra su relevancia en el mundo científico y tecnológico.
Descubre la clave: números racionales vs irracionales
La diferencia fundamental entre los números racionales e irracionales radica en su capacidad de expresión mediante fracciones. Mientras que los números racionales pueden ser representados como cocientes de números enteros, los irracionales no pueden ser expresados de esta forma y requieren notaciones especiales como raíces o constantes matemáticas.
Relación con los números enteros y fraccionarios
Los números irracionales son una extensión de los números enteros y fraccionarios, ampliando el espectro numérico y permitiendo abordar problemas matemáticos más complejos. Esta relación entre los diferentes tipos de números es esencial para comprender la estructura y jerarquía del conjunto numérico.
Preguntas frecuentes sobre números irracionales
¿Cuál es la diferencia entre un número irracional y un número racional?
La principal diferencia radica en su representación: los números racionales pueden expresarse como fracciones, mientras que los irracionales no pueden ser representados de esa manera y tienen expansiones decimales infinitas no periódicas.
¿Todos los números irracionales son trascendentes?
No, no todos los números irracionales son trascendentes. Algunos números irracionales, como √2, son algebraicos, lo que significa que son raíces de ecuaciones polinómicas con coeficientes enteros.
¿Cuál es la importancia de los números irracionales en matemáticas?
Los números irracionales son fundamentales para completar el conjunto de números reales y resolver problemas matemáticos avanzados. Su presencia en diversas ramas de las matemáticas demuestra su relevancia y utilidad en el desarrollo teórico y aplicado.
¿Por qué se llaman «irracionales» si no tienen relación con la lógica?
El término «irracional» en el contexto de los números se refiere a la imposibilidad de expresar estos números de manera «racional» con fracciones simples. Aunque el nombre puede parecer contradictorio, se basa en la definición matemática de estos números como no racionales.