Descubre la razón detrás del nombre de los números complejos
Los números complejos son una extensión de los números reales que incluyen una parte imaginaria. Aunque el término «complejo» puede sonar intimidante, en realidad hace referencia a la combinación de dos partes: la parte real y la parte imaginaria. Esta dualidad es lo que da origen al nombre de números complejos.
La complejidad de los números complejos
A pesar de su nombre, los números complejos no son necesariamente más complicados que los números reales. De hecho, una vez que se entiende su estructura, los números complejos se vuelven herramientas poderosas en matemáticas, física, ingeniería y otras disciplinas.
El significado matemático de «complejo»
En matemáticas, el término «complejo» se utiliza para denotar la presencia de dos partes: la parte real, que corresponde a los números reales que ya conocemos, y la parte imaginaria, que se expresa en términos de la unidad imaginaria «i». Esta combinación de partes da lugar a un número complejo en forma a + bi, donde «a» es la parte real y «bi» es la parte imaginaria.
Descubre el fascinante origen de los números complejos
Los números complejos tienen un origen histórico interesante que se remonta a la necesidad de resolver ecuaciones que no tenían solución en el conjunto de los números reales. Fue en el siglo XVI cuando los matemáticos comenzaron a explorar la posibilidad de ampliar los números reales para abarcar un conjunto más amplio de soluciones.
Los inicios de los números complejos
El matemático italiano Rafael Bombelli fue uno de los pioneros en el estudio de los números complejos. En su obra «L’Algebra», publicada en 1572, Bombelli introdujo por primera vez la noción de números complejos y desarrolló técnicas para operar con ellos. Aunque en su época fueron recibidos con escepticismo, con el tiempo los números complejos se convirtieron en una herramienta invaluable en matemáticas.
La evolución de la notación
A lo largo de los siglos, la notación utilizada para representar los números complejos ha ido evolucionando. Desde la introducción de la unidad imaginaria «i» por Bombelli, hasta la notación actual de a + bi, los matemáticos han refinado la forma de expresar y operar con números complejos.
Descubre por qué los números complejos son imaginarios
Aunque el término «imaginario» pueda sugerir que los números complejos no son reales, en realidad forman parte de un sistema matemático coherente que incluye tanto la parte real como la parte imaginaria. La inclusión de la parte imaginaria en los números complejos permite resolver ecuaciones que de otra manera no tendrían solución en el conjunto de los números reales.
La importancia de la parte imaginaria
La parte imaginaria de un número complejo se expresa en términos de la unidad imaginaria «i», que se define como la raíz cuadrada de -1. Esta introducción de un nuevo elemento en los números complejos amplía significativamente las posibilidades de cálculo y resolución de ecuaciones.
Operaciones con números complejos
Al operar con números complejos, es importante tener en cuenta tanto la parte real como la parte imaginaria. Las operaciones básicas, como la suma, resta, multiplicación y división, se realizan teniendo en cuenta ambas partes del número complejo. El resultado final es un número complejo que combina las partes real e imaginaria de acuerdo a las reglas establecidas.
Descubre qué son los números complejos con ejemplos
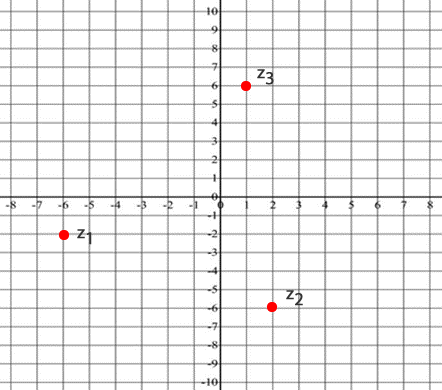
Los números complejos se representan en forma a + bi, donde «a» es la parte real y «bi» es la parte imaginaria multiplicada por la unidad imaginaria «i». Esta representación permite visualizar los números complejos en un plano cartesiano, donde el eje horizontal corresponde a la parte real y el eje vertical a la parte imaginaria.
Visualización en el plano complejo
Al representar los números complejos en un plano cartesiano, se pueden identificar patrones y relaciones entre los diferentes números complejos. Por ejemplo, la distancia de un número complejo al origen del plano se conoce como el módulo, y la fase es el ángulo que forma el número complejo con el eje horizontal.
Ejemplos de operaciones con números complejos
Para comprender mejor cómo funcionan los números complejos, veamos algunos ejemplos de operaciones básicas:
- Suma: (2 + 3i) + (1 + 2i) = 3 + 5i
- Resta: (5 – 2i) – (3 + i) = 2 – 3i
- Multiplicación: (2 + i) * (3 – 2i) = 8 – i
- División: (4 + 5i) / (2 – i) = (3.2 + 2.6i)
Preguntas frecuentes sobre números complejos
¿Qué es la parte imaginaria de un número complejo?
La parte imaginaria de un número complejo se expresa en términos de la unidad imaginaria «i» y representa la componente no real del número.
¿Por qué se utilizan los números complejos en matemáticas?
Los números complejos se utilizan en matemáticas para resolver ecuaciones que no tienen solución en el conjunto de los números reales, ampliando así las posibilidades de cálculo y análisis matemático.
¿Cómo se representan los números complejos en un plano cartesiano?
Los números complejos se representan en un plano cartesiano donde el eje horizontal corresponde a la parte real y el eje vertical a la parte imaginaria del número complejo.
¿Cuál es la importancia de la unidad imaginaria «i» en los números complejos?
La unidad imaginaria «i» es fundamental en los números complejos, ya que permite introducir la parte imaginaria y resolver ecuaciones que de otra manera no tendrían solución en el conjunto de los números reales.
¿Qué aplicaciones tienen los números complejos en la vida real?
Los números complejos tienen aplicaciones en campos como la física, la ingeniería, la electrónica y la teoría de números, donde se utilizan para modelar fenómenos y resolver problemas que involucran cantidades complejas.