Descubre el origen del término seno
El término «seno» en trigonometría proviene del latín «sinus», que a su vez deriva del vocablo sánscrito «jiva». En la antigüedad, los matemáticos hindúes utilizaban la palabra «jiva» para referirse a la cuerda que une el arco de un círculo con su extremo, concepto fundamental en trigonometría.
Descubre el significado del seno en trigonometría
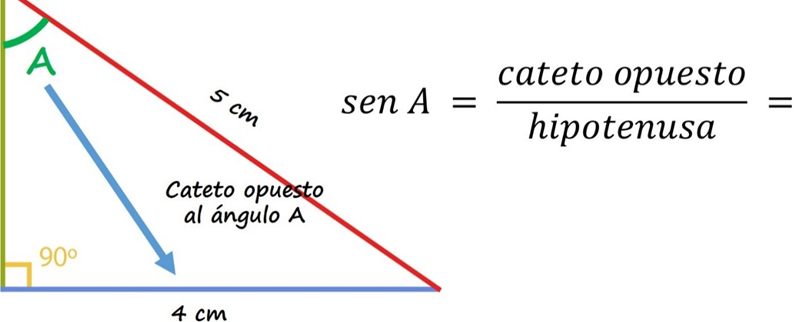
En trigonometría, el seno de un ángulo en un triángulo rectángulo se define como la razón entre la longitud del cateto opuesto a dicho ángulo y la hipotenusa del triángulo. Matemáticamente, se expresa como:
sen(θ) = Cateto opuesto / Hipotenusa
Donde θ representa el ángulo en cuestión.
Descubre el origen de seno, coseno y tangente
Los términos «seno», «coseno» y «tangente» fueron introducidos por el matemático persa Al-Biruni en el siglo XI. Al-Biruni tradujo del sánscrito al árabe varios tratados matemáticos hindúes, donde se utilizaban estos conceptos trigonométricos. Posteriormente, estos términos fueron adoptados por matemáticos europeos durante la Edad Media.
Descubre por qué se llaman razones trigonométricas
Las funciones trigonométricas como el seno, coseno y tangente se denominan «razones trigonométricas» debido a que representan la relación entre las longitudes de los lados de un triángulo rectángulo. Estas razones son fundamentales para resolver problemas relacionados con medidas de ángulos y distancias en geometría y física.
Importancia del seno en trigonometría
El seno es una función trigonométrica fundamental que permite calcular la altura de un objeto, la distancia recorrida por un proyectil en movimiento parabólico, la amplitud de una onda senoidal, entre otros conceptos matemáticos y físicos.
Relación entre seno, coseno y tangente
El seno, el coseno y la tangente están estrechamente relacionados a través de identidades trigonométricas como la identidad pitagórica, la suma de ángulos y la resta de ángulos. Estas relaciones permiten simplificar cálculos y resolver ecuaciones trigonométricas de manera más eficiente.
Aplicaciones del seno en la vida cotidiana
El seno se aplica en campos tan diversos como la ingeniería, la arquitectura, la astronomía, la navegación marítima, la geodesia y la física, donde su uso es imprescindible para el diseño de estructuras, la predicción de mareas, la localización de objetos celestes y la medición de distancias.
Preguntas frecuentes
¿Cuál es la relación entre el seno y el coseno?
El seno y el coseno son funciones trigonométricas complementarias, es decir, el coseno de un ángulo es igual al seno del ángulo complementario y viceversa. Esta relación se basa en la identidad fundamental sen²(θ) + cos²(θ) = 1.
¿Por qué es importante el seno en la resolución de triángulos?
El seno es fundamental en la resolución de triángulos ya que permite calcular la longitud de un lado desconocido a partir de un ángulo y un lado conocido, aplicando la ley de senos o la ley de cosenos según el caso.
¿Cómo se relaciona el seno con las funciones periódicas?
El seno es una función periódica con un período de 2π, lo que significa que se repite cada 360 grados o cada 2π radianes. Esta propiedad lo convierte en una herramienta útil para modelar fenómenos cíclicos como el movimiento armónico simple o las oscilaciones en sistemas físicos.
¿Cuál es la importancia histórica del seno en el desarrollo de las matemáticas?
El concepto de seno ha sido fundamental en el desarrollo de la trigonometría y la geometría desde la antigüedad, permitiendo a matemáticos y científicos resolver problemas relacionados con la medición de ángulos, distancias y movimientos en el espacio. Su influencia se extiende a disciplinas como la física, la ingeniería y la astronomía.
¿Cómo se calcula el seno de un ángulo en la actualidad?
Actualmente, el seno de un ángulo se calcula utilizando calculadoras científicas, programas de software matemático o tablas trigonométricas, que facilitan la obtención de valores precisos en diferentes unidades de medida como grados, radianes o gradianes.